Master PRMIA 8010 Exam with Reliable Practice Questions
Which of the following formulae describes Marginal VaR for a portfolio p, where V_i is the value of the i-th asset in the portfolio? (All other notation and symbols have their usual meaning.)
A)
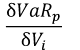
B)

C)
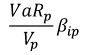
D) All of the above
Correct : D
Marginal VaR of a component of a portfolio is the change in the portfolio VaR from a $1 change in the value of the component. It helps a risk analyst who may be trying to identify the best way to influence VaR by changing the components of the portfolio. Marginal VaR is also important for calculating component VaR (for VaR disaggregation), as component VaR is equal to the marginal VaR multiplied by the value of the component in the portfolio.
Marginal VaR is by definition the derivative of the portfolio value with respect to the component i. This is reflected in Choice 'a' above. Using the definitions and relationships between correlation, covariance, beta and volatility of the portfolio and/or the component, we can show that the other two choices are also equivalent to Choice 'a'.
Therefore all the choices present are correct.
Start a Discussions
Which of the formulae below describes incremental VaR where a new position 'm' is added to the portfolio? (where p is the portfolio, and V_i is the value of the i-th asset in the portfolio. All other notation and symbols have their usual meaning.)
A)
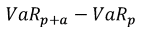
B)
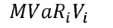
C)

D)
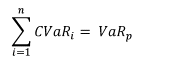
Correct : A
Incremental VaR is the change in portfolio VaR resulting from a change in a single position. This is accurately described by VaR_(p+a) - VaR_p. The other answers are incorrect, and describe other concepts.
It is important to know and understand the ideas behind MVaR (marginal VaR), CVaR (component VaR) and iVaR (incremental VaR), and the differences between them.
Start a Discussions
Which of the following are true:
1. The total of the component VaRs for all components of a portfolio equals the portfolio VaR.
2. The total of the incremental VaRs for each position in a portfolio equals the portfolio VaR.
3. Marginal VaR and incremental VaR are identical for a $1 change in the portfolio.
4. The VaR for individual components of a portfolio is sub-additive, ie the portfolio VaR is less than (or in extreme cases equal to) the sum of the individual VaRs.
5. The component VaR for individual components of a portfolio is sub-additive, ie the portfolio VaR is less than the sum of the individual component VaRs.
Correct : D
Statement I is true - component VaR for individual assets in the portfolio add up to the total VaR for the portfolio. This property makes component VaR extremely useful for risk disaggregation and allocation.
Stateent II is incorrect, the incremental VaRs for the positions in a portfolio do not add up to the portfolio VaR, in fact their sum would be greater.
Statement III is correct. Marginal VaR for an asset or position in the portfolio is by definition the change in the VaR as a result of a $1 change in that position. Incremental VaR is the change in the VaR for a portfolio from a new position added to the portfolio - and if that position is $1, it would be identical to the marginal VaR.
Statement IV is correct, VaR is sub-additive due to the diversification effect. Adding up the VaRs for all the positions in a portfolio will add up to more than the VaR for the portfolio as a whole (unless all the positions are 100% correlated, which effectively would mean they are all identical securities which means the portfolio has only one asset).
Statement V is in incorrect. As explained for Statement I above, component VaR adds up to the VaR for the portfolio.
Start a Discussions
Which of the following is not a measure of risk sensitivity of some kind?
Correct : A
Measures of risk sensitivity include delta, gamma, vega, PV01, convexity and CR01, among others. They allow approximating the change in the value of a portfolio from a change (generally small) in one of the underlying risk factors.
Risk sensitivity measures are derivatives of the value of the portfolio, calculated with respect to the risk factor. Some risk sensitivity measures are second derivatives, and allow a more precise calculation of the change in the value of the portfolio. Many risk sensitivities are represented by Greek letter, but not all.
Delta () is a measure of the change in portfolio value based on a 1% change in the value of the underlying. Gamma () is a second order derivative that improves the calculation as part of a Taylor expansion. CR01 is a measure of the change due to a 1 basis point change in the credit spread. PL01 is not a measure of any kind of risk sensitivity, it does not mean anything.
Start a Discussions
Which of the following belong to the family of generalized extreme value distributions:
1. Frechet
2. Gumbel
3. Weibull
4. Exponential
Correct : B
Extreme value theory focuses on the extreme and rare events, and in the case of VaR calculations, it is focused on the right tail of the loss distribution. In very simple and non-technical terms, EVT says the following:
1. Pull a number of large iid random samples from the population,
2. For each sample, find the maximum,
3. Then the distribution of these maximum values will follow a Generalized Extreme Value distribution.
(In some ways, it is parallel to the central limit theorem which says that the the mean of a large number of random samples pulled from any population follows a normal distribution, regardless of the distribution of the underlying population.)
Generalized Extreme Value (GEV) distributions have three parameters: (shape parameter), (location parameter) and (scale parameter). Based upon the value of , a GEV distribution may either be a Frechet, Weibull or a Gumbel. These are the only three types of extreme value distributions.
Start a Discussions